16.1 Induction of labor.
(A)
1 = 1 / 111 = 0.0090, or 0.9% and
2 = 13 / 117 = 0.1111, or 11.1%
(B)= 0.08. Induction was associated with a 92% reduction in risk.
(C) 95% confidence interval for RR: ln= -2.526; se = 1.029; 95% CI for lnRR = -2.526 � (1.96)(1.029) = -2.526 � 2.017 = (-4.543, -0.509); 95% CI for RR = (0.01, 0.60).
16.3 HIV infection among women entering the New York State Correctional System
(A)
1 = 61 / 136 = 0.4485 [approx. 45%] and
2 = 27 / 339 = 0.0796 [approx. 8%]
(B)
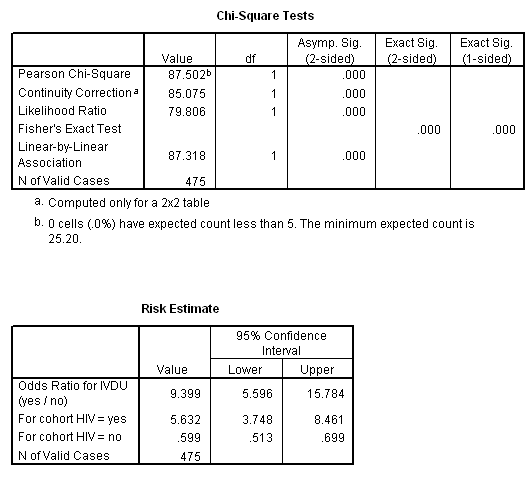
= 0.4485 / 0.796 = 5.6315 @ 5.63. Interpretation: You could say prevalence in the IVDU+ group is 5.63 times that of the IVDU- group. You could also say prevalence is 463% greater with IVDU+. Some of you may be tempted to say there is a strong positive association between IVDU and HIV. This is OK as long as you also quantify the relation in one form or an other. Relation between prevalence ratios and risk ratios: Prevalence ratios are equal to risk ratio when certain assumptions are met. The assumptions are: (a) duration of disease is similar in the groups, (b) disease is rare, and (c) disease does not influence the exposure (Rothman and Greenland, 1998, p. 64). In the current problem, the disease is not rare, so the prevalence ratio is not a risk ratio.
(C) 95% confidence interval: ln
= ln(5.6315) = 1.728; selnf^ = 0.208; 95% CI for lnf = 1.728 � (1.96)(0.208) = (1.321, 2.137); 95% CI for f = e(1.321, 2.137) = (3.75, 8.47). This allows us to say with 95% confidence that the prevalence ratio parameter lies between 3.75 and 8.47. Some epidemiologists would interpret these limits as a "best-case scenario / "worst-case scenario." In addition, the confidence interval "length" is a direct measure of the precision of the estimate. In any event, we say confidently that the prevalence ratio is between 3.75 and 8.47. Of course, this statement assumes data are valid.
(D) H0: RR = 1 versus H1: RR
1; Expected frequencies (below) exceed 5, making Fisher's test unnecessary; Yates' chi-square = 85.08 with 1 df, P = 0.0000. The association is significant (Reject H0). Calculations shown below:
D+ D-
E+ 25.196 110.804 136
E- 62.804 276.196 339
88 387 475c2Yates' = (|61 - 25.196| - 0.5)2 / 25.196 + (|75 - 110.804| - 0.5)2 / 110.804 +
(|27 - 62.804| - 0.5)2 / 62.804 + (|312 - 276.196| - 0.5)2 / 276.196
= 49.468 + 11.249 +
19.846 + 4.513
= 85.075(E) SPSS output
(F) Sample size requirements: I used WinPepi (below) and assumed p2 = 0.08 (based on
2 above). To detect an RR of 2, n1 = n2 = 489
(G) To detect an RR of 1.5, n1 = n2 = 1663
16.5 Cytomegalovirus and coronary restenosis.
(A)
= (21/49) / (2/26) = 0.4286 / 0.0769 = 5.571. Risk in the CMV+ group is 5 to 6 times that of the CMV- group
ln= ln(5.571) = 1.717; SE = 0.6992; 95% confidence interval = e (0.3486, 3.0894) = (1.42, 21.93).
Interpretation: Several points should be made. The magnitude of the risk ratio should be noted (i.e., The imprecision of the estimate (broad confidence interval) should also be noted. It is also important to note that data support the CMV / restenosis hypothesis.(B) X2stat, c = 8.29, df = 1, P = 0.0040; significant evidence against H0.
16.7 Oral contraceptives and myocardial infarction.
(A) 2-by-2 table
HD+ HD-
OC+ 13 4987 5000
OC- 7 9993 10000(B)
= (13/5000) /(7/10000) = 3.714; SE = 0.468; 95% confidence interval for the lnf = ln(3.714) � (1.96)(0.468) = (0.395, 2.229); 95% confidence interval for f = e(0.395, 2.229) = (1.48, 9.30). The risk ratio point estimate is suggestive of almost 4 times the risk in the oral contraceptive group. The broad confidence interval suggests this estimate is not very precise.
(C) H0:RR = 1 versus H1: RR
1; X2stat c-c = 7.67, df = 1; P = 0.0056. The evidence against H0 is significant
16.9 Kayexelate and colonic necrosis
(A) Determine the incidence of colonic necrosis in the groups.
1 = 2 / 117 = 0.017;
2 = 0 / 862 = 0.000
(B) Calculate expected cell counts. [Below] Which test would you use with these data? Fisher's exact or the Mid-P exact
Expected
Necrosis + Necrosis - Generic +
0.24 116.67 Generic -
1.76 860.24
(C) Calculate and report an appropriate P value. Calculated with www.OpenEpi.com: Fisher's P (two-sided) = 0.028; Mid-P P = 0.014
16.11 Contingency tables involving small numbers (3-by2).
(A) You cannot use a chi-square test because two of the table cells have expected values that are less than 5 (see below).
Expected
Normal teeth Malocclusion
1.739 18.261 Bottle fed 1.913 20.087 Brst +bottle
4.348 45.652 (B) Fisher's P = 0.1503; Mid-P P = 0.1390
[Advanced users: X2stat = 4.154; df = 2, P = 0.125, which is not too different from the Mid-P value. Here's another interesting fact: only 8 of 92 subjects (9%) had normal teeth--perhaps the Austin Power's movies were not exaggerating the state of British dental health in the 60s!]
16.13 Don't sweat the small stuff or P = 0.05. X2stat = 4.107, df = 1; P = 0.043; X2stat, c = 3.598, df = 1; P = 0.058. Although the regular chi-square statistics produces a P value that is a little below 0.05 and the continuity-corrected chi-square statistic produces a P-value that is a little above 0.05, it would not be reasonable to derive different conclusions from the same data. There is nothing sacred about either of these test statistics or alpha = 0.05. Both tests provide fairly good evidence against the null hypothesis.
16.15 Do seatbelt laws prevent injury? Display the data in a 2-by-2 table [below] and compare the incidence of "no injury" to injury" in the form of a risk ratio and interpret these results. RR = 1.023, indicating a 2.3% increase in the "no injury" rate. Include a 95% confidence interval... (1.006, 1.04)
|
|
Injury |
|
|
|
|
No |
Yes |
Total |
|
After |
1281 | 103 | 1384 |
|
Prior |
6596 | 694 | 7290 |
|
Total |
7877 | 797 | 8674 |
16.17 Anger and heart disease (hard outcome, hypertensives).
Calculate risk ratios for
(A) moderate-anger vs. low-anger 0.83
(B) high-anger vs. low-anger. 1.01
(C) Does a dose-response pattern seem to emerge? No