12 Key, Odd

Review Questions

1. grand
2. group
3. �_i and _i, respectively
4. True.
5. H₀: �₁ = �₂ = . . . = �_k  (equivalently, H₀: s²_Between s²_Within)
6. df_B = 4-1 = 3; df_w = 32-4 = 28
7. The dependent variable is glucose level. The independent variable is the sex of the taxi driver.
8. the grand mean 
9. nominal . . . scale (although ordinal data can also be analyzed). 
10. independent t test (assuming equal variance)
11. 
12. _i 
13. within
14. df_w 
15. greater than
16. df_B 

Exercises

12.1 Weight gain and junk food. The dependent variable is weight gain (grams) and the independent variable is diet type (1 = standard diet, 2 = junk food, 3 = health food). The study was done in laboratory mice (for obvious reasons); there are 5 mice per group (small sample). The study was set up to learn about the effect of diet on weight gain.

(A) Means and standard deviations 

n₁ = 5, ₁ = 11.14, s₁ = 1.27
n₂ = 5, ₂ = 13.44, s₂ = 0.623 
n₃ = 5, ₃ = 9.14, s₃ = 0.581

(B) Boxplot:  Locations (averages) demonstrate clear differences. The small samples ( n_i = 5) preclude robust statements about shape and location.

(C) Replicate descriptive statistics and boxplot in SPSS
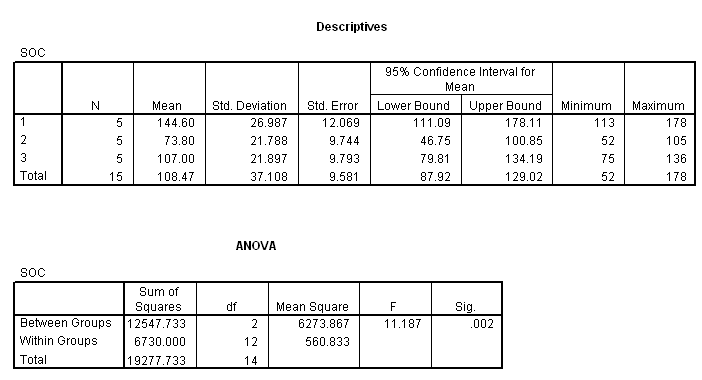
(D) ANOVA calculations

• H₀: �₁ = �₂ = �₃ vs. at least one of the population means is different
• SS_B = (5)(11.14 - 11.24)² + (5)(13.44 - 11.24)² + (5)(9.14 - 11.24)² = 0.05 + 24.20 + 22.05 = 46.30
• df_B = 3 - 1= 2
• s²_B = 46.30 / 2 = 23.15
• SS_W = (5-1)(1.27)² + (5-1)(0.623)² + (5-1)(0.581)² = 6.452 + 1.553 + 1.350 = 9.37
• df_W = 15 - 3 = 12
• s²_{W =} 9.37 / 12 = 0.78
• F_stat = 23.15 / 0.78 = 29.69

• To determine the approximate P-value, draw the F_2,12 curve and then look up the landmark for alpha = 0 .05 in the F table, which is  F_2,12,.95 = 3.89. You should place the landmark on the curve, noting that the area under the curve to the right of this landmark is .05. Then put the F_stat (which is 29.69) far to the right of the landmark. The area under the curve to the right of the F_stat should be shaded to represent the p value. It should be clear now that p < .05.  The precise P-value (StaTable)  @ 0.000. 

• The conclusion is to reject H₀ and conclude the average differed significantly.

ANOVA table:

Source      SS    df       MS    
Between  46.30     2    23.15
Within    9.37    12      .78     

(E) Replicate ANOVA in SPSS.

12.3 Maternal adaptation.

(A) Explore the data with side-by-side boxplots. The SPSS boxplots are shown below. (The labels on the X-axis failed to print in the transfer to html. Here are the group descriptions we are going to have to keep in mind when interpreting these data: Group 1 = LBW + intervention, Group 2 = LBW + no intervention, Group 3 = normal birth weight, no intervention.)

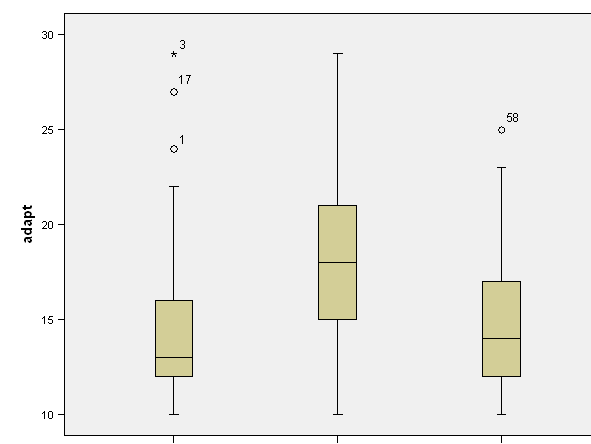
Report the most salient findings from this exploration. Side-by-side boxplots reveal outside values in Group 1 (LBW + intervention) and Group 3 (normal BW + no intervention). Group 2  (LBW + no intervention) shows higher average values than both Group 1 or Group 3.

What do you make of the outside values? These outside values represent women with high scores -- women having excessive trouble adapting to motherhood -- and should be investigated.  

(B) Group summary statistics are given in the problem. Construct a one-way ANOVA table based on thee summary statistics.  See below.

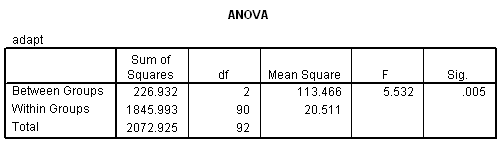
Report the F statistic and P-value used to test H₀: �₁ = �₂ = �_3.  F_stat = 5.53 with 2 and 90 df; P = 0.005.  Therefore, the difference among groups is significant.

(C) In rejecting H₀, are you concluding that all three groups differ?  No!

12.5 Sense of coherence 

(A) Boxplots