2 = 13.44, s2 =
0.623). The smallest, in the health food
group (3 = 9.14, s3 = 0.581).
Results in the standard diet group were intermediate (
1 = 11.14, s1 = 1.27). All three groups had five
observations (n1 = n2 = n3
= 5). The ANOVA table was:13.1 Weight gain and junk food. Last week's analysis of
the data set deermice.sav
revealed a significant difference in weight gain in three groups feed different
diets. The greatest
weight gain occurred in the junk food group (2 = 13.44, s2 =
0.623). The smallest, in the health food
group (3 = 9.14, s3 = 0.581).
Results in the standard diet group were intermediate (
1 = 11.14, s1 = 1.27). All three groups had five
observations (n1 = n2 = n3
= 5). The ANOVA table was:
Source SS df MS F
Between 46.30 2 23.15 29.69
Within 9.37 12 .78(A) Conduct post hoc comparison using the least square difference method. It is OK to assume homoscedasticity. [For each comparison, semean dif =
(0.780 * (1/5 + 1/5)) = 0.5586]
(B) Incorporate Bonferroni's adjustment into each of the post hoc comparisons.
(C) Download the data set deermice.sav (right-click > Save as) and replicate the analyses in SPSS (Analyze > Comparison of Means > One-way ANOVA > Post Hoc).
(D) ANOVA addresses random error only. We are also concerned about bias. List the three types of systematic errors (biases) that may effect statistical analyses.
(E) In addition to the validity assumptions, ANOVA has distributional and sampling assumptions. Name these.
(F) Test the groups for unequal variance using Levene's output from SPSS. (Click the Options button and check the homogeneity of variance box.) Show all hypothesis testing steps.
(G) Conduct a Kruskal-Wallis test with SPSS by clicking Analyze > Non-Parametric Tests > k Independent Samples. The test variable is WTGAIN and the group variable is GROUP. You must define the range of the independent variable with the Define button (minimum is 1, maximum is 3). Under the null hypothesis, the Kruskal-Wallis statistic has a chi-squared distribution with k - 1 degrees of freedom. Interpret your results.
13.2 Fever reduction.
Analysis of this data in the prior unit revealed a significant difference in fever
reduction between aspirin (1
= 1.50 oF), aspirin
and acetaminophen (2
= 0.36 oF), and acetaminophen
alone (3 = 0.08
oF). Each group had 5 observations.
The ANOVA Fstat was 6.52 with 2 and 12 df (P = 0.012).
The mean square within (s2w ) was 0.4338.
Conduct post hoc comparisons of the results using Bonferroni's method. Show all
work and interpret your results.
13.3 The problem of multiple comparisons. When two or more events are independent, their probabilities may be multiplied to determine the probability of their joint occurrence. For example, if event A and event B are independent, then their joint probability is Pr(A) � Pr(B). If events A, B, and C are independent, then their joint probability is Pr(A) � Pr(B) � Pr(C). For this problem we will suppose the probability of making a correct decision in each instance is 0 .99. The exercise will show how the probability of making at least one false decision is large when making a large family of decisions.
(A) What is the probability of making 3 correct independent decisions in a row? What is the probability of getting at least 1 of the three wrong? [Note: Pr(at least one wrong) = 1 - Pr(all correct).]
(B) What is the probability of making 10 correct independent decisions in a row? What is the probability of getting at least 1 wrong out of the 10?
(C) What is the probability of making 20 correct independent decisions in a row. What is the probability of making at least one incorrect decisions out of the 20?
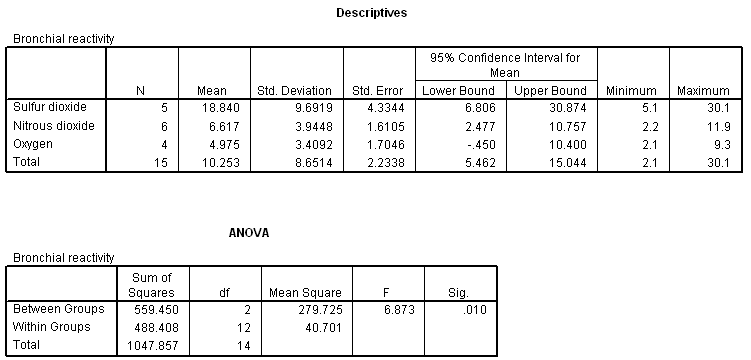
13.4 Bronchial reactivity. An exercise in the prior chapter looked at bronchial reactivity in asthmatics following exposure to noxious gases. The analysis revealed significant differences in airway reactivity. Summary statistics and the ANOVA results are shown below. Now conduct post hoc comparisons using the LSD method (bronch-react.sav). In each instance, state the null hypothesis, test statistic, df, and P value. Interpret each test.
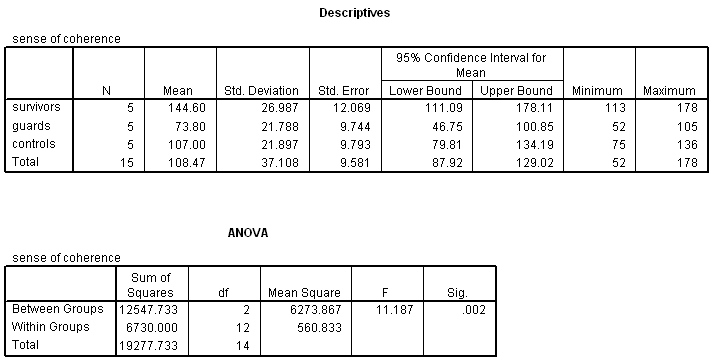
13.5 Sense of coherence. Summary statistics and an ANOVA table for the "sense of coherence" data (soc.sav) introduced in the prior chapter are shown below. Conduct post-hoc comparisons using a Bonferroni adjustment. Summarize the results.
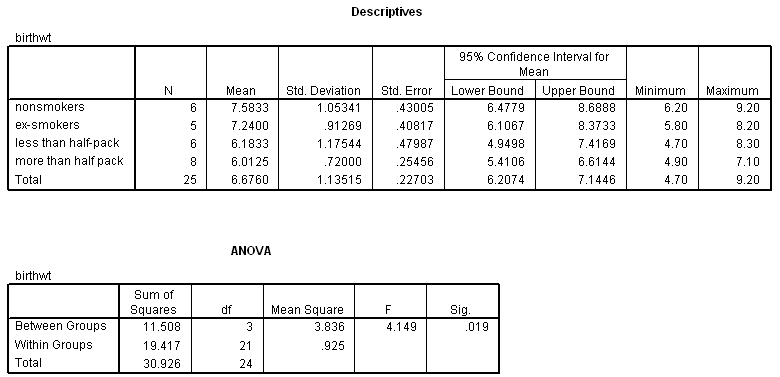
13.6 Smoking and birth weight. This data set (smoking-moms.sav) was introduced in the prior chapter. Descriptive statistics and the ANOVA table for the problem are reported below. Conduct post hoc comparisons of all the groups with the LSD method. (There are 6 possible post-hoc comparisons.) State the null hypothesis in each instance, report the t statistics, their df, and P value. Interpret each test.
13.7 Maternal adaptation (Howell, 1995, pp. 302 - 304; mat-role.sav). Place-holder...
13.8 - 13.20 Reserved for future use.
13.21 Testosterone levels in roosters (visual inspection of boxplots). A zoologist wanted to determine if testosterone in three strains of mature roosters differed (Hampton, 1994, p. 147). Data are:
Strain A: 439 568 134 897 229 329
Strain B: 103 115 098 126 115 120
Strain C: 107 099 102 105 089 110Here are side-by-side boxplots of the data:
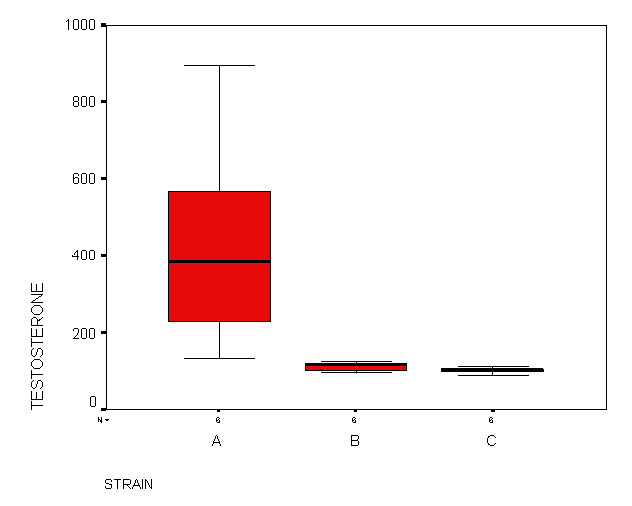
Based on this evidence, would you perform ANOVA? Explain your reasoning.
13.22 Testosterone levels in roosters (K-W procedure). Download rooster.sav (right-click > Save as). Conduct a Kruskal-Wallis procedure on the data with the help of SPSS. List the hypotheses (null and alternative), test statistic, and its df, and your conclusion.
13.23 Smoking and birth weight (assess homoscedasticity). Return to the data discussed in Exercise 13.6 (smoking-moms.sav). A colleague suggests you have violated the equal variance assumption. Rebut this criticism by interpreting the relevant information n the descriptive statistics table that appears as part of Exercise 13.6.
13.24. Smoking and birth weight (Levene's). Support the equal variance claim you made in Exercise 13.23 with Levene's procedure. List the null and alternative hypothesis, the test statistic and its dfs, and your conclusion. (Use SPSS for computations smoking-moms.sav.)
13.25. Smoking and birth weight (K-W). To appease your critic, you conduct a non-parametric test (even though it is not required). Conduct a K-W procedure, and compare its results to those achieved by one-way ANOVA.
Key to Odd Numbered Exercises Key Even Numbered Exercises (may not be posted)