17: Case-Control Studies (Odds Ratios) 4/7/07

Review Questions

1. How do case-control studies differ from cohort studies?
2. Why are case-control studies unable to estimate incidence or prevalence?
3. What symbol is used to denote the odds ratio parameter? What symbol is used to denote the odds ratio estimator?
4. Before calculating a confidence interval for the odds ratio, we converts the odds ratio estimate to a ______________ scale.
5. What is the value of the odds ratio parameter under the null hypothesis?
6. When is Fisher's test used in place of a chi-square test?
7. In a  2-by-2 table for  matched-pair data, table cells t and w contain counts for ____________ pairs, while cells u and v contain counts for ___________ pairs.
8. True or false? In matched case-control studies, information about concordant pairs is ignored.
9. What is the name of the chi-square statistic used to test matched-pair data?
10. What is the primary benefit of matching?
11. [T or F?] You can use a 95% confidence for the odds ratio to determine statistical significance at alpha = 0.05.
12. [T or F?] You can use a 95% confidence for the odds ratio to determine statistical significance at alpha = 0.01.
13. How do you use a 95% confidence for the odds ratio to determine statistical significance at alpha = 0.05?
14. Which of the following 95% confidence interval for odds ratios are significant at alpha = 0.05? (a) 0.01 to 0.77 (b) 0.77 to 1.23 (c) 1.23 to 2.43

Exercises

Part A: Independent Samples

17A.1 Cell phones and brain tumors, Study 1. A case-control study by  Inskip and co-workers (2001) examined cellular telephone use and intracranial tumors. The study was completed between 1994 and 1998 and included 782 cases with various types of intracranial tumors and 799 controls admitted to the same hospitals for a variety of nonmalignant conditions. Subjects were classified as exposed if they reported use of a cellular telephone for more than 100 hours. The odds ratios (95% confidence intervals) calculated by the study were: for glioma 0.9 (0.5 to 1.6), for meningioma:  0.7 (0.3 to 1.7), for acoustic neuroma: 1.4 (0.6 to 3.5), for all tumor types combined: 1.0 (0.6 to 1.5). Do these results support or fail to support the theory that recent hand-held cellular telephones use causes brain tumors? Explain your response.

17A.2. Cell phones and intracranial tumors, study 2. A different case-control study on intracranial tumors and cell phone use by Muskat and co-worker (2000)[full text] was completed between 1994 and 1998. This study used a structured questionnaire to quantify the statistical relation between cell phone use and primary brain cancer in 469 cases and 422 controls. The results of the study stated "The median monthly hours of use were 2.5 for cases and 2.2 for controls. Compared with patients who never used handheld cellular telephones, the multivariate odds ratio (OR) associated with regular past or current use was 0.85 (95% confidence interval 0.6 to 1.2). The OR for infrequent users (<0.72 h/mo) was 1.0 (95% confidence interval 0.5 to 2.0) and for frequent users (>10.1 h/mo) was 0.7 (95% confidence interval 0.3 to 1.4). The mean duration of use was 2.8 years for cases and 2.7 years for controls. The OR was less than 1.0 for all histologic categories of brain cancer except for uncommon neuroepitheliomatous cancers (OR, 2.1; 95% confidence interval 0.9 to 4.7)." Interpret the results of this study. Are they materially different from the study described in Exercise 17A.1?

Note 1: The studies described in the prior two exercises looked at many types of intracranial tumors (e.g., gliomas, meningiomas, neuromas, epitheliomas, and so on). Different tumor types have different biology and are likely to have different causes. Therefore, pooling results as done in these studies is questionable.

Note 2: Without experimentation, or large effects, statistics can play only a modest role in determining causal relations. Therefore, other information must come into play. In the two prior exercises, for example, we must consider that the type of energy emitted by cell phones is non-ionizing. Non-ionizing radiation does not cause damage to chemical bonds or to DNA. If we  combine with the negative evidence from the epidemiologic studies with these biologic facts, it seems unlikely that cell phones can cause brain tumors. 

17A.3 Esophageal cancer and tobacco use (same as lab exercise). Data come from the same case-control study on esophageal cancer considered earlier in this chapter. In this analysis we look at tobacco use dichotomized at 20 gms/day. [Data are originally from Tuyns and coworkers (1977) as reported by Breslow and Day (1980). Individual data records for the data set are stored online in the data file bd1.sav as variables TOB2 and CASE] Cross-tabulation reveals:

(A) Calculate the odds ratio for the data and a 95% confidence interval for the odds ratio parameter. Interpret these statistics. 
(B) Calculate a P value for the problem. Interpret this statistic.
(C) Download bd1.sav. and open it in SPSS. Create the code book for the data file by clicking File > Display Data Info > bd1.sav > OK. Keep the codebook handy for future reference. 
(D) Cross-tabulate the data in SPSS (Analyze > Descriptive Statistics > CrossTabs).  Select TOB2 as the row variable and CASE as the column variable. Click the statistics button and check the boxes for Chi-square and Risk . Click Continue > OK. Make certain you confirm these results with your hand calculations. 

17A.4  IUDs  and infertility. A case-control study of contraceptive devices and infertility found prior use of intra-uterine devices (IUDs) in 89 of 283 infertile cases. In contrast, 640 of 3833 fertile control women had used IUDs (Cramer et al., 1985; Rosner, 1990, p. 381).  Data are shown in a 2-by-2 table, below. Calculate the odds ratio and its 95% confidence interval. Interpret the results.

17A.5 Doll & Hills, 1950.  A important study in the history of case-control methods was completed in 1950 by Doll & Hill. This study found that 647 of the 649 lung cancer cases were smokers. In contrast, 622 of 649 controls smoked. (Click here for a reprint of the original article.) 

(A) Display data in 2-by-2 cross-tabulation of the counts
(B) Calculate the odds ratio and its 95% confidence interval. 
(C) Interpret the results. 

17A.6 Brain tumors and electric blanket use. A case-control study assessed the risks of brain tumors associated with electric blanket use. Cross-tabulated data are shown below. Calculate the odds ratio and its 95% confidence interval. Interpret your findings. 

Source: Preston-Martin et al., 1996 . Data are stored as individual records in the data file BRAINTUM.SAV

17A.7 Vasectomy and prostate cancer. Data from a case-control study on vasectomy and prostate cancer are cross-tabulated below (Zhu et al., 1996). Calculate the odds ratio and its 95% confidence interval. Interpret your findings. (Optional: Calculate the P value for the problem.)

17A.8 Asbestos, cigarettes, and lung cancer. By going through the steps listed below, you will learn how to detect statistical interaction. Data stored in asbestos.sav are from a case-control study on lung cancer, asbestos  exposure, and smoking. Right-click the file name to download the dataset. 

(A) Cross-tabulate LUNGCA (column) by SMOKE (row). Determine the odds ratio.
(B) Cross-tabulate LUNGCA by ASBESTOS. Determine the odds ratio.
(C) Cross-tabulate LUNGCA by ASBESTOS stratified by SMOKE. This is accomplished by filling in the SPSS dialogue box as shown below. Calculate the odds ratios for smokers and non-smokers separately. Are these odds ratios homogeneous? What is the effect of asbestos in smokers? ... in non-smokers?

17A.9 Esophageal cancer and alcohol recorded at four levels. The data set BD1 was introduced earlier in these notes. Recall that this is a case-control study of esophageal cancer. In this analysis, alcohol consumption is  recorded at four levels: 0-39 g/day, 40-79 g/day, 80-119 g/day, and 120+ g/day. Cross-tabulated results follow: Calculate the odds ratio associated with each level of alcohol consumption. Is there evidence of a dose-response relationship? 

Hint: To analyze these data, you can break it up into the four 2-by-2 cross-tabulations (shown below):

17A.10 Wynder and Graham's case-control study of smoking and lung cancer. A historically important case-control study on smoking and lung cancer compared smoking histories of 605 cases with lung cancer to 780 non-cancer controls (Wynder & Graham, JAMA, 1950). Data on average tobacco use during the past 20 years are:  

^* If subject smoked for less than 20 years, the amount of smoking
was reduced in proportion to duration.

(A) Calculate odds ratio for each level of smoking using the non-smokers as the reference group. (Optional: Determine 95% confidence intervals for each estimate.) 
(B) Advanced: Test the data for trend.

17A.11 Baldness and myocardial infarction, self-assessed baldness. Both baldness and myocardial infarction (heart attacks) are more common in males than in females. Is there a link between the two? The answer to this question takes on additional importance when one considers treatments for baldness such as minoxidil. If the underlying condition of baldness elevated cardiovascular disease risk, then any increase in the risk observed in minoxidil users might mistakenly be attributed to the drug and not to the underlying condition of baldness (so-called confounding by indication). A case-control study addressed the relation between nonfatal myocardial infarction and baldness. Cases were men under 55 years of age admitted to hospitals in Massachusetts and Rhode Island for a first heart attack with no prior history of serious heart problems. Controls were men admitted to the same hospitals for non-fatal, non-cardiac problems. Control subjects with a prior history of heart disease were excluded from the study. Data for the distribution of baldness according to patients' self-assessments graded on a scale of 1 (no baldness) to 5 (extreme baldness) are shown below (Lesko and co-workers, 1993; Table 6).

 

Baldness	Cases*	Controls
1 (none)	251	331
2	165	221
3	195	185
4	50	34
5 (extreme)	2	1
Total	663	772

* 2 cases had missing exposure data

(A) Calculate odds ratios associated with each level of baldness using baldness level 1 as the reference category. Interpret these results.
(B) Perform a chi-square test for association  Report the chi-square statistic, its df and P-value. Interpret the results.
(C) Advanced students: Perform a Mantel test for trend. 
(D) Differences besides those have to due with hirsuteness were found between cases and controls. For example, the median age of case was 47 years, while the median age of controls was 43 year. Explain why this is important. 
(E) Because they were concerned about the potentially confounding effects of age and other factors, the investigators adjusted for age, race, religion, years of education, body mass index, use of alcohol and cigarettes, family history of myocardial infarction, history of angina, hypertension, diabetes, hypercholesterolemia, and gout, exercise, personality, number of doctor visits in prior year with multivariate logistic regression model. The multivariate adjusted ORs and crude ORs are listed below. Does this materially effect you interpretation of results?

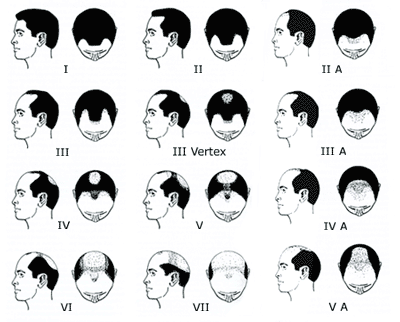
17A.12. Baldness and myocardial infarction, interviewer assessed baldness. This exercise is a continuation of the Exercise 17A.11. In addition to using self-assessments of baldness (by study subjects), the study in question used interviewer assessments of baldness based on the Hamilton baldness scale. Here are the data according the this measurement of the explanatory variable: Baldness Cases* Controls** None a 238 480 Frontal b   44 82 Mild vertex c 108 137 Mod. vertex d 40 46 Severe vertex e 35 23 Total  465 768 * 200 cases had missing data; ** 4 controls had missing data. a = Hamilton baldness categories I and II on the modified  b = Hamilton categories IIa, III, IIIa, and IVa. c = Hamilton categories III and IV d = Hamilton categories V and Va. e = Hamilton categories VI and VI [Source: Table 5 in Lesko et al., 1993] (A) Compare the assessments of baldness used in this analysis to the self-assessments used in Exercise 17A.11. Which method is preferable? (Explain your reasoning.) How could misclassification of baldness affect the results of the study? (B) Calculate the odds ratios associated with each level of exposure.  (C) Compare these results to those of the prior exercise.

Part B: Matched-pairs

17B.1 Fruits, vegetables, and adenomatous polyps (same as lab exercise). A case-control study by Witte and co-workers (1996) used matched-pairs to study the risk of adenomatous polyps of the colon in relation to diet. All cases and controls had undergone sigmoidoscopic screening. Controls were matched to cases on time of screening, clinic, age, and sex. One of the study's analyses considered the effects of low fruit and vegetable consumption on colon polyp risk. There were 45 pairs in which the case but not the control reported low fruit/veggie consumption. There were 24 pairs in which the control but not the case reported low fruit/veggie consumption [Summary counts reported in Rothman & Greenland, 1998, p. 287; same data as StatPrimer illustrative example.]

(A) Calculate the odds ratio associated with low fruit/veggie consumption. Interpret this result. 
(B) Calculate a 95% confidence interval for the odds ratio. Interpret this result. 
(C) Calculate a P value for testing H₀: OR = 1.
(D) Do data support a connection between low fruit/veggie consumption and colon cancer?

17B.2 Smoking and mortality in identical twins. When smoking was first suspected as a cause of disease, Sir Ronald Fisher offered the constitution hypothesis as an explanation for the observed association. Fisher (1957, 1958a, 1958b) did not entirely dispose of the causal hypothesis, however.)  The constitutional hypothesis suggested that people genetically disposed to lung cancer were more likely to smoke. In other words, the relation between smoking and disease was confounded by constitutional factors. The constitutional hypothesis was put to the ultimate test by a study in which 22 smoking-discordant monozygotic twins where studied to see which twin first succumbed to death (Kaprio & Koskenvuo, 1989). In this study, the smoking-twin died first in 17 of the pairs (i.e., u = 17, while u + v = 22). Calculate the odds ratio for these data. In addition, calculate a P-value for testing H₀: OR = 1. Is the constitutional hypothesis refuted? 

17B.3 Thrombotic stoke in young women. The Collaborative Group Study of Stroke in Young Women (1975) used case-control sampling to study cerebrovascular disease (stroke) and oral contraceptive use in women between 14- to 44-years. Cases were matched to controls according to neighborhood, age, sex, and race.  Here are the matched data for the thrombotic stroke cases from the study (Lilienfeld & Lilienfeld, 1980, p. 220): 

Matched-pairs	Control E+	Control E-	Total
Case E+	2	44	46
Case E-	5	55	60
Total	7	99	106

(A) Calculate the odds ratio for these data.
(B) Now suppose the match was broken and investigators had analyzed the data unaware of the importance of matched analysis. Rearrange the information from the above matched-pair table to show how it would appear in an unmatched 2-by-2 cross-tabulation. Notice that there are 106 pairs, so make certain your 2-by-2 table shows results for all 212 individuals. Then, calculate the odds ratio for the data with the match broken. How does this odds ratio compare to that of the (proper) matched-pair odds ratio? 

17B.4 Hemorrhagic stoke in young women. Exercise 17B.3 introduced data from the  Collaborative Group Study of Stroke in Young Women. The outcome in this prior exercise was thrombotic stroke. Now we consider hemorrhagic stroke. Matched data are shown below. "Break the match" and then rearrange the data into a 2-by-2 cross-tabulation, (A total of 310 individuals should appear in this table.) Calculate odds ratios for both the matched and unmatched data. How do results compare? 

17B.5 Estrogen and cervical cancer. Data from a matched case-control study of conjugated estrogen use and cervical cancer by Antunes and co-workers (1979) are  shown below (Abramson & Gahlinger, 2001, p. 137). 

(A) Calculate the odds ratio and its 95% confidence interval. Interpret your results. 
(B) Calculate a P value for the problem

Key to Odd Numbered Problems                                              Key to Even Numbered Problems (may not be posted)