15: Regression (Key Odd)

Review Questions

  1. The primary difference is that regression provides a measure of the functional relationship between X and Y in terms of expected change in Y per unit increase in X.
  2. With algebraic models, all points fall on the line. With statistical models, points scatter about the line randomly. Statistical models are used to predict the expected value of Y, not the exact value. This is aided by addressing the residuals around the proposed line.
  3. The slope represents the angle of the line (change in Y per unit X). The intercept represents the point at which the line crosses the Y-axis (when X = 0).
  4. A slope of zero indicates no change in Y per unit X.
  5. The residuals are squared in a least squares line.
  6. For each year of age we expect an additional 1.5 inches in height (on the average). = 44 + 1.5(10) = 44 + 15 = 59 inches.
  7. t25-2,.975 = t23,.975 = 2.07
  8. sample slope = b. population slope = beta
  9. n - 2
  10. decrease
  11. residual 
  12. Confounding is a distortion of a statistical relationship caused by an extraneous factor.
  13. residuali = yi - i where i is the predicted value of Y for observation i
  14. Linearity, independence, Normality, equal variance 
  15. Vocabulary

Exercises

15.1 Anscombe's quartet. 

(A) Plot each data set ...

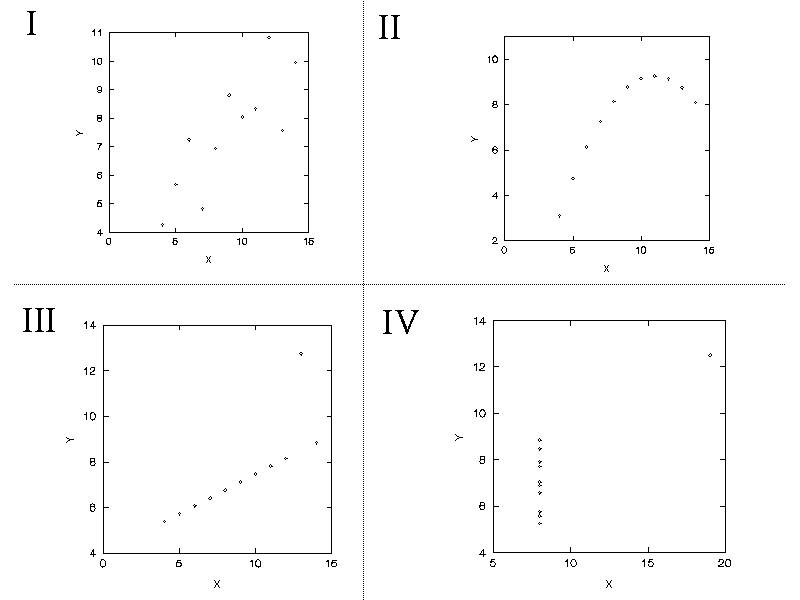
(B) Which data sets will support linear correlation and regression? Although all the data sets show interesting relationships, none can be adequately described by a straight line except data set 1. Linear correlation and regression are appropriate only for data set 1. 

15.3 Ecological study of smoking and lung cancer. 

(A) Calculate the least square regression coefficients for these data. Then show the regression model (equation) for the data.    = 6.79 + (0.0228)X  
(B) Interpret the slope estimate of the model. The slope predicts 0.0228 additional cases per 100,000 person-years for each additional cigarette smoked per capita. This corresponds to an increase of 2.28 cases per 100,000 person-years for each additional 100 cigarettes smoked per capita. 
(C) Predict the lung cancer mortality rate (per 100,000 person-years) in a country with annual per capita cigarette consumption of 800 cigarettes. = 6.79 + (0.0228)(800) = 25.03 [per 100,000 p-yrs]
(D) Calculate the 95% confidence interval for the slope  sY|x = ([1375 - (0.0228)(32717)]/9) = 8.360; SEb = 8.360 / (1432255) = 0.00699; 95% CI for b = 0.0288 � (t9,.975)(0.00699) = 0.0288 � (2.26)(0.00699) = 0.0288 � 0.0159 = (0.0070, 0.0386). Interpret this interval. We can say with 95% confidence the slope in the population (beta) is no less than 0.0070 and is no more than 0.0386.
(E) SPSS results...

15.5  Gravid iguanas.

(A) Calculate least squares regression estimates a and b. = 1.432 + 31.89X  Interpret the slope coefficient. How much would a 0.1 kg. increase in body weight increase eggs production. This model predicts an increase of 31.89 of eggs per kg of iguana body weight. Proportionally this translates to an additional 3.189 eggs per 0.1 kg of body weight.
(B) H0: b = 0 versus H0: b   0; t stat is used: seb = 3.883; tstat = 31.89 / 3.883 = 8.21; df = 9 - 2 = 7, P 0; highly significant.
(C) What is the predicted number of eggs for a 1.2 kg iguana? = 1.432 +(31.89)(1.2) = 45.67 

15.7 Water fluoridation and dental cavities. 
(A) Data

(B) Untransformed data Interpretation: 

Any outliers? Yes. Lower left quadrant -- a city with low fluoride and low cavity rate. (Observation 21 with coordinates 0.1, 37) 
[I have since discovered that the outlier was a data entry problem. The correct value is (0.1, 1037). The data point will not be correct for this exercise, but it will be excluded.] 

Relation linear? No! [Curvilinear, yes.]

Relation? The scatter plot reveals an strong curved negative relation between fluoride levels and cavity rates. The steepest decline occurs between 0 and 1 ppm of fluoride. The decline levels off after this point.

Unmodified linear regression would not be warranted under these circumstances (two reasons -- non-linearity and outlier).
(C) Outlier removed + ln-ln transformated data

Interpretation:

Relation linear? Yes. This relation can be described by a straight line. 

Correlation statistics: 
r = 0.97 
r2 = 0.95 
Very strong positive correlation, excellent model fit (95% of variation in Y explained by X).

Regression equation:
ln() = 5.805 + (-0.409)lnX


Interpretation of slope: For each increase ln(ppm fluoride), 0.409 decline is ln(cavities per 100 children).
(D) Outlier removed + range restricted 

Interpretation:

Relation linear? Not perfectly, but good enough for descriptive purposes.

Correlation statistics: 
r = 0.93
r2 = 0.86
Strong correlation; good fit, but not as good as ln-ln transform. Notice the hook toward the higher values of X.

.

Regression model:
= 780.34 + (-528.1)x

Comment: Although the fit of this model is not as good as model B, I  prefer no model. The untransformed figure shows most clearly that the decline in cavity rates is steep in the 0 to 0.8 range. Since higher levels have only modest increases in benefit and potential toxicity, any action should be devoted to adding less than 1  ppm of fluoride to public water sources.